FPB dan KPK

A. Faktor Persekutuan Terbesar(FPB)

adik-adik !

sebelum kita mempelajari tentang FPB, kita perlu tahu nih apa itu FPB. Hmmmmmmm......... apa yah FPB itu?yukk mari kita pelajari bersama.

Faktor Persekutuan Terbesar(FPB) adalah bilangan bulat positif terbesar yang bisa membagi habis 2, 3 atau seterus dari bilangan itu. tapi sebelum kita belajar lebih lanjut, kita perlu tahu juga nih apa itu faktor bilangan, faktor persekutuan, dan faktorisasi prima.

1. Faktor Bilangan

Faktor bilangan merupakan bilangan yang dapat membagi habis bilangan tertentu.

misalnya

a. Berapakah faktor bilangan dari 8

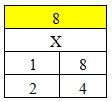
Maka faktor bilangan dari 8 adalah 1, 2, 4, dan 8.

b. Berapakah faktor bilangan dari 12?

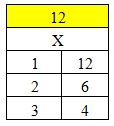
Maka faktor bilangan dari 12 adalah 1, 2, 3, 4, 6, dan 12.

2. Faktor persekutuan

Faktor persekutuan merupakan faktor yang sama dari dua bilangan atau lebih. Untuk menentukan faktor persekutuan dari 2 bilangan atau lebih tersebut kita bisa mengikuti langkah langkah berikut ini;

a. Carilah faktor bilangan dari masing-masing bilangan tersebut.

Misalnya:

Faktor dari 8 adalah 1, 2, 4, 8.
Faktor dari 12 adalah 1, 2, 3, 4, 6, 12.

b. Carilah bilangan yang sama dari kedua faktor bilangan tersebut.

Misalnya:

Faktor dari 8 adalah 1, 2, 4, 8.
Faktor dari 12 adalah 1, 2, 3, 4, 6, 12.

Maka faktor persekutuan dari 8 dan 12 adalah 1, 2, dan 4.

3. Faktor Prima

Faktor prima merupakan faktor dari suatu bilangan yang berupa bilangan prima. Sedangkan bilangan prima yaitu bilangan yang hanya memiliki 2 faktor yakni bilangan itu sendiri dan juga 1 (satu).

Sebagai contoh :

a. Faktor dari 8 adalah 1, 2, 3, 4, 6, 12.

Dari faktor bilangan di atas yang berupa bilangan prima adalah 2. Maka faktor prima dari 8 adalah 2.

b. Faktor dari 12 adalah 1, 2, 3, 4, 6, 12.

Dari faktor bilangan di atas yang berupa bilangan prima adalah 2 dan 3. Maka faktor prima dari 12 adalah 2 dan 3.

Untuk membantu kita dalam mencari faktor prima dari suatu bilangan, maka kita bisa memakai pohon faktor atau dengan cara sengkedan (tusuk sate).

Perhatikan contoh di bawah ini!

Berapakah faktor prima dari 8 dan 12 ?

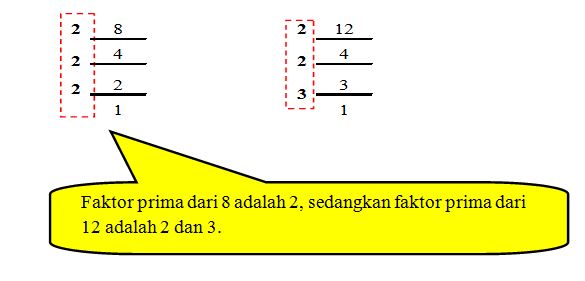
Perlu diketahui bahwa di dalam mencari faktor prima suatu bilangan, jika faktor prima tersebut ganda atau lebih dari satu maka cukup ditulis satu saja. Contoh pada faktor dari 8 didapat 2, 2, 2, maka cukup ditulis 2 saja.

nah, setelah kita mengetahui apa itu FPB, Faktor bilangan, Faktor Persekutuan, dan Faktor Prima. saatnya kita akan belajar cara mencari FPB.

Seperti pepatah mengatakan kalau ada banyak cara menuju Roma maka dalam FPB ada banyak cara yang dapat kita lakukan untuk mencari FPB. 

Cara 1: mencari FPB dengan cara mendaftar faktor persekutuannya

Misalnya:

Berapa FPB dari 8 dan 12?

Faktor dari 8 adalah 1, 2, 4, 8.
Faktor dari 12 adalah 1, 2, 3, 4, 6, 12.

Faktor persekutuan dari 8 dan 12 adalah 1, 2, dan 4.
Maka FPB dari 8 dan 12, kita ambil bilangan yang terbesar adalah 4.

Cara 2: Menggunkan tabel

carilah FPB dari 8 dan 12 dengan menggunakan tabel!

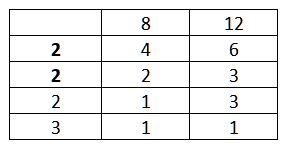
Dari tabel tersebut di atas, untuk mencari FPB kita menggunakan bilangan yang bisa dibagi untuk keduanya, yaitu ternyata 2 x 2 (lihat yang dicetak tebal). Jadi, dapat kita simpulkan bahwa FPB dari 8 dan 12 adalah 4.

Cara 3: Menggunakan pohon faktor

Carilah FPB dari 8 dan 12 menggunakan pohon faktor !

Dari pohon faktor di atas maka didapatlah:

• Faktorisasi prima dari 8 adalah 2 x 2 x 2 atau 2³
• Faktorisasi prima dari 12 adalah 2 x 2 x 3 atau 2² x 3

Setelah itu kita :

• Mencari faktor prima yang sama yaitu 2 ( 2² dan 2³),
• Memilih yang berpangkat paling kecil yaitu antara 2² dan 2³ yang paling kecil yaitu 2².
  Jadi FPB dari 8 dan 12 adalah 2² atau 4.

Cara 4: Menggunakan sengkedan

Misalnya:

Carilah FPB dari 8 dan 12 menggunakan cara sengkedan !

FPB dari 8 dan 12 bisa dilihat bilangan yang ada di sebelah paling kiri yaitu 2 dan 2 artinya 2 x 2 = 4.

B. Kelipatan Persekutuan Terkecil( KPK)

Sebelum kita lanjut... kita perlu tahu apa itu kelipatan bilangan, kelipatan persekutuan bilangan, dan faktorisasi prima( yang sudahdi bahas dalam FPB).

1. Kelipatan bilangan

Kelipatan merupakan hasil perkalian suatu bilangan dengan bilangan asli yang lainnya.

Misalnya:

• Kelipatan dari 3 adalah 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36. . . dst.
• Kelipatan dari 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 . . . dst

2. Kelipatan persekutuan bilangan

Kelipatan Persekutuan Bilangan merupakan hasil kelipatan yang sama dari beberapa bilangan.

Misalnya:

• Kelipatan dari 3 adalah 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36. . . dst.
• Kelipatan dari 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 . . . dst.

Maka kelipatan persekutuan dari 3 dan 4 yaitu 12, 24, 36 dan seterusnya.

Nah, agar pemahaman kita tentang KPK makin mantap! mari kita lihat cara kerja beserta contoh dari KPK dibawah ini.

Cara 1: Menggunkan pohon faktor

Carilah KPK dari 6 dan 8 dengan pohon faktor!

6 = 2 x 3

8 = 2 x 2 x 2 atau 2³.

Langkah-langkah dalam mencari Kelipatan Persekutuan Terkecil (KPK)

• 1) Carilah faktorisasi prima dari masing-masing bilangan tersebut.
• 2) Tulislah semua faktor prima yang ada.
• 3) Apabila terdapat faktor prima yang sama, pilihlah faktor prima yang berpangkat paling besar.

Faktorisasi prima dari 6 adalah 2 x 3.
Faktorisasi prima dari 8 adalah 2 x 2 x 2 = 2³.

Kita tulis semua faktornya : 2 x 3 x 2³
Terdapat faktor prima yang sama yaitu 2 dan 2³, kita pilih yang berpangkat terbesar yaitu 2³.
Kita kalikan faktor primanya 2³ x 3 = 8 x 3 = 24.
Jadi KPK dari 6 dan 8 adalah 24.

Cara 2: Menggunakan sengkedan atau tusuk sate

Untuk cara mencari KPK dengan tusuk sate atau sengkedan ini hampir sama dengan saat kita mencari FPBnya di awal. Namun untuk mencari KPK ini pembaginya tidak harus bisa membagi habis semua bilangan, 1 saja sudah boleh digunakan untuk membagi. Dan perlu diingat, semua bilangan harus sampai habis terbagi atau nilainya (1).

Misalnya:

Tentukan KPK dari 6 dan 8 dengan cara sengkedan atau tusuk sate!

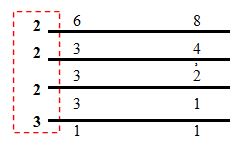
KPK dari 6 dan 8 cukup kita ambil bilangan yang diberi tanda lingkaran merah dan mengalikannya. Sehingga menjadi 2 x 2 x 2 x 3 atau 2³ x 3 = 8 x 3 = 24.

Nah, untuk lebih memahami materi yukkksimak video dibawah ini!

sumber

https://penapengajar.com/materi-kpk-dan-fpb-kelas-4/